The interactions between electric currents and magnets are described by Maxwell’s equations, which, since their derivation in the 19th century, have set the basis for all electrodynamical phenomena. However, our understanding of electromagnetism remains limited by our understanding of the electron.
As surprising as it may sound, no one really knows what an electron is. And it is this fundamental mystery that has been the driving force for much of modern physics and what eventually led to the development of quantum field theory.
To answer the question “What is an electron?”, you would think the first step would be to observe it. However, that is easier said than done. Electrons are simply too small for us to observe—the smallest thing we can observe is an atom, and even that cannot be observed with a traditional microscope.
So, while we can’t observe an electron, we can observe its behavior—more specifically its energy. Currently this is done with Penning traps—a special device developed in the 1970s with the purpose of trapping particles for extensive periods of time so that accurate measurements could be made.
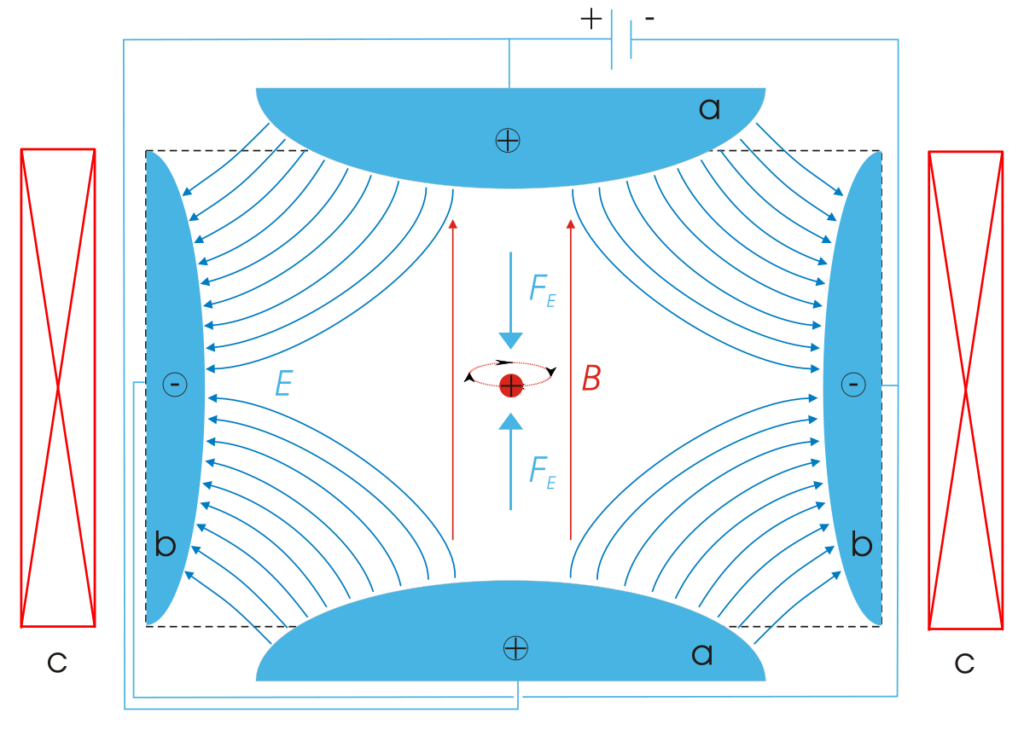
What is important to note is that when we make such a measurement of the energy, we are in fact making a measurement of a single ion, i.e., an electron surrounding a central nucleus, not a single electron. In fact, it was this type of energy measurement that led to the discovery of the electron by J. J. Thompson in 1879.
J.J. Thompson
This discovery subsequently ended the idea that the atom was the smallest particle, with Thompson instead suggesting that an atom is composed of electrons surrounded by a soup of positive charge—the plum pudding model. However, this was later found to be incorrect when Ernest Rutherford carried out his famous gold leaf experiments along with Geiger and Marsden, and concluded that the mass of an atom was concentrated at its center, and thus proposed a model with a positive central nucleus surrounded by negatively charged electrons.
Rutherford Experiment
This model was further developed with the help of Niels Bohr, but instead of the electrons being randomly distributed, he proposed that they existed in orbitals—orbiting the central positive nucleus in a manner analogous to planets orbiting a central star.
Now, with any model we should be able to explain what we are observing. A spectral analysis of hydrogen, for example, reveals a set of discrete emission lines which the Bohr model explains as the transition of electrons between orbitals.
However, the Bohr model is only able to explain the emission spectra for hydrogen or other single electron atoms like ionized helium. For multi-electron atoms the spectral analysis showed many more discrete emission lines that could not be explained by the Bohr model. This is where the quantum model took over, where, instead of existing in precisely-defined orbits, all that is known about electrons is their probable distribution around the atom—generally referred to as an electron cloud. The electron cloud model was developed in 1926 by Erwin Schrödinger and Werner Heisenberg, and can be explained in terms of a probability wave—specifically the Schrodinger wave equation—where the states or “orbitals” that an electron can occupy in an atom is analogous to that of a standing wave.
In the quantum model, these states, or orbitals, depend on a set of quantum numbers; for example, the principle quantum number n, the angular momentum number l, the magnetic number m, and the spin number s. It is these different quantum numbers that define the position and momentum of an electron in terms of a probability cloud, and thus describe the emission lines that were unaccounted for in the Bohr model. The quantum model was also extended to explain emission lines that occur due to an external magnetic field and/or due to interactions with the quantum vacuum.
This alternative view of electrons as probability clouds, rather than definite orbital states, successfully describes the behavior of matter. However, although achieving what the Bohr model couldn’t, it still doesn’t reveal the nature of the electron and where its mass comes from. The question “What is an electron?” becomes ever more paramount with increasing technological advancements and corresponding limits to design. For example, Moore’s Law states that the number of transistors in a dense integrated circuit doubles roughly every two years. But at what point would this scaling end? This is one of the important questions in semiconductor physics, and one that physicist Carver Mead set about answering through considerations of electron tunneling. However, contrary to the assumption of the time, Mead argued that as transistors decreased in size, they would also get faster, better, cooler, and cheaper. In 1972, Mead and graduate student Bruce Hoeneisen predicted that transistors could be made as small as 0.15 microns, which, in the year 2000, was actually realized. But just how much smaller could they get?
To get deeper still we need a model that more accurately describes the nature and structure of the electron, which is precisely what is offered in the generalized holographic model introduced by Nassim Haramein. This approach starts by defining the fundamental bit of energy as an oscillating spherical unit at the Planck scale—named the Planck Spherical Units (PSU). Then, expanding on the work of physicists David Bohm, Jacob Bekenstein, Stephen Hawking, Gerard ’t Hooft, and Leonard Susskind, it states that the energy—or information— of any spherical system is proportional to the number of PSUs within the spherical volume (volume entropy) and the number of PSUs available on the spherical surface horizon (surface entropy). This holographic relationship between the exterior and the interior defines the mass expressed by the system at any given moment, while the inverse defines the mass-energy density of the system—or as described by David Bohm, the unfolded and the enfolded, respectively. The question is, can this approach be extended to the electron?
The first step in answering this question is to consider the spatial extent of the electron and the volume of information that it encloses. So if we start with the premise that an electron cloud can be considered as an “electron” coherent field of information, then instead of thinking about the electron as a separate system, the electron could be thought of as a cloud of potential energy spatially extending from the proton out to the radius where the volume encloses the electron cloud of a hydrogen Bohr atom. When we utilize this approach, we find an electron mass solution in terms of the holographic surface-to-volume ratio—the transfer potential—and a mass equivalent to the experimentally measured mass of the electron. So now we have a model that not only predicts the correct mass of the electron but also offers a physical understanding of its structure down to the scale of the Planck length.
This model is in line with Carver Mead’s approach to electrodynamics—collective electrodynamics—which, instead of utilizing Maxwell’s equations, sees all electrodynamical behaviour as resulting from interactions of the wavefunctions of electrons behaving collectively. He states the best example of this is the semiconductor, which exhibits a coherent, collective state of matter, and thus represents a quantum system on a grand scale.
This new picture of the electron as a coherent collective behaviour of the Planck scale granular structure of spacetime is non-trivial, as not only does it give us a deeper understanding of the nature of the electron, it can also help deepen our understanding of semiconductor physics. The details of this work were recently published in Physics Essays.
About the Author
Dr Amira Val Baker is a research scientist at Torus Tech laboratories and affiliate of the Unified Science Institute (USI), formerly the Hawaii Institute for Unified Physics (HIUP). Her work focuses on black holes from a unified physics perspective which sees black holes as the connecting factor between subatomic matter and cosmology. Amira graduated with an Msci in Astrophysics from UCL (University College London) where her Master thesis was on the modelling of UV irradiance levels and ozone layer depletion trends. She holds a PhD in Astrophysics from the Open University under the supervision of Dr Andrew Norton and on the topic of high-mass x-ray binary stars, neutron stars, and black holes.
Prior to joining Torus Tech laboratories, she completed post-doctoral research at the University of Alicante in Spain, as part of the Massive Stars group, where one of her group publications was highlighted in the National Geographic article, “Astronomers Spy Monster Star Merger on the Move.”
As a scientist Amira has a deep passion for education developed through her work as a science tutor, teacher, and coordinator in science education and publication with experience working at the Gatsby Science Enhancement Programme and the Royal Society Publishing.
In her spare time, she can be found enjoying good food, practising martial arts, archery, horse riding, and traveling alongside her husband, Ariffin.
